Introduction

Consider a system of two-dimensional linear equations:

$a_1x + b_1y = c_1$

$a_2x + b_2y = c_2$

Note that here, $x$ and $y$ are two separate variables representing two separate attributes, while the rest are constants. Drawing from Linear Combinations of Vectors, we can rewrite the given system using vectors such that each vector has two dimensions, one for representing the first equation and the other for representing the second equation (in the same order for all the vectors). This is given below:

$\begin{bmatrix} a_1 \newline a_2 \end{bmatrix} x + \begin{bmatrix} b_1 \newline b_2 \end{bmatrix} y = \begin{bmatrix} c_1 \newline c_2 \end{bmatrix}$

Putting $\vec{a} = \begin{bmatrix} a_1 \newline a_2 \end{bmatrix}$, $\vec{b} = \begin{bmatrix} b_1 \newline b_2 \end{bmatrix}$ and $\vec{c} = \begin{bmatrix} c_1 \newline c_2 \end{bmatrix}$, we get:

$\vec{a} x + \vec{b} y = \vec{c}$

Visualisation

For visualisation, consider the following system:

$2x + y = 3$

$x - 2y = -1$

Hence, we get $\vec{a} = \begin{bmatrix} 2 \newline 1 \end{bmatrix}$, $\vec{b} = \begin{bmatrix} 1 \newline -2 \end{bmatrix}$ and $\vec{c} = \begin{bmatrix} 3 \newline -1 \end{bmatrix}$.

We can recognise two ways of visualising this system:

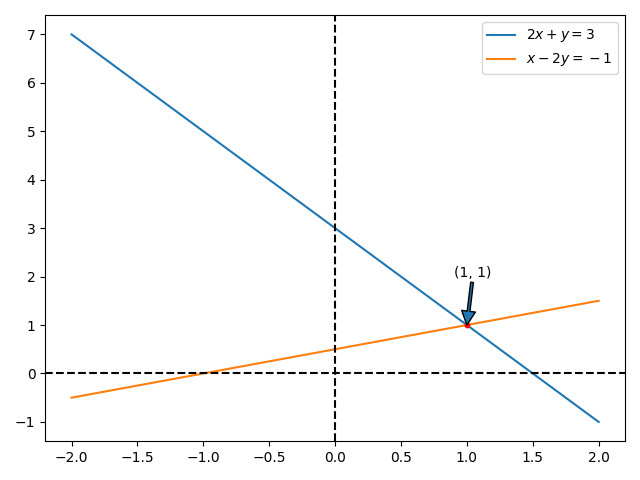
1. Row picture

One equation at a time
Each equation is a function in a 2D space
Intersection of the functions is the solution

Row Picture

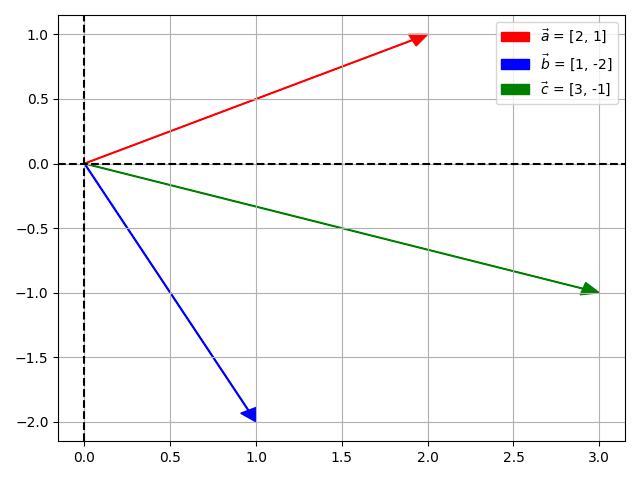
2. Column Picture

One vector at a time
Each vector is drawn in a 2D space
$\vec{c}$ is the resultant vector
The solution is the linear combination of $\vec{a}$ and $\vec{b}$ that reaches $\vec{c}$

Column Picture

Code for Graph Generation »

Generalisation for $n$-dimensional space

Consider a system of $k$ $n$-dimensional linear equations:

$a_{11}x_1 + a_{12}x_2 … + a_{1n}x_n = c_1$

$a_{21}x_1 + a_{22}x_2 … + a_{2n}x_n = c_2$

…

$a_{k1}x_1 + a_{k2}x_2 … + a_{kn}x_n = c_k$

For convenience, put:

$\vec{a_1} = \begin{bmatrix} a_{11} \newline … \newline a_{k1} \end{bmatrix}$, $\vec{a_2} = \begin{bmatrix} a_{12} \newline … \newline a_{k2} \end{bmatrix}$ … $\vec{a_n} = \begin{bmatrix} a_{1n} \newline … \newline a_{kn} \end{bmatrix}$

Also for convenience, put:

$\vec{c} = \begin{bmatrix} c_1 \newline … \newline c_k \end{bmatrix}$

1. Row Picture:

One equation at a time
Each equation is a function in an $n$-dimensional space
Intersection(s) of the functions is/are the solution(s)

2. Column Picture:

One vector at a time
Each vector is drawn in an $n$-dimensional space
$\vec{c}$ is the resultant vector
Solutions are linear combinations of $\vec{a_1}, \vec{a_2} … \vec{a_n}$ that reach $\vec{c}$